Who Is the People? Pt. 2

What a voting system does is map individual preferences to a collective decision. If we were to sit down and design a voting system, what properties should we require? What would make it a sound mechanism for measuring the Will of the People?

Condorcet’s Paradox

The first person to analyze voting systems and develop a theory of social choice was the Marquis de Condorcet, an 18th-century French mathematician and philosopher. As part of his work, Condorcet described a paradox in collective decision-making.

Suppose we have three candidates \(a,b,c,\) and three voters each with different preferences: voter 1 ranks \(a>b>c\), voter 2 ranks \(b>c>a\), and voter 3 ranks \(c>a>b\).

Two voters (a majority) prefer \(a\) to \(b\), and two voters prefer \(b\) to \(c\), but two voters also prefer \(c\) to \(a\). The social preference would appear to be cyclical: \(a>b>c>a\).

The voters express their preferences completely and unambiguously, and yet the social ordering is worse than ambiguous: it’s contradictory!

A Fair and Reasonable Voting System

Problems like Condorcet’s paradox tell us that designing a good voting system maybe isn’t as trivial as we might like. If we want a voting system to be fair and reasonable, we should be precise about just what that means and specify the conditions to satisfy.

Here is a version of the list of desirable conditions first suggested by Kenneth Arrow in 1950:

1. Rationality. The output of our voting system is a weak ordering, i.e., a ranking of the candidates by preference (or indifference—hence “weak”). We want to avoid the cyclical problem of Condorcet’s paradox.
2. Determinism. The outcome is a result of voter preferences, not other factors. Selecting elected officials by lottery might be fair in the sense that flipping a coin is fair, but it doesn’t really meet our goal of turning voter preferences into a collective decision.
3. Unanimity. If all voters prefer Antiphon to Clodius, then the collective decision made by the voting system should prefer Antiphon. (This is sometimes called a Pareto condition.)
4. Independence of Irrelevant Alternatives. The social preference between two candidates should be independent of preferences for other candidates. If we prefer Antiphon to Clodius, the social preference between those two shouldn’t be changed by our opinion of Daniel Webster.
5. Non-Dictatorship. The collective decision is not the choice of a single voter, i.e., a dictator. If I prefer Antiphon to Daniel Webster, and everybody else prefers Daniel Webster to Antiphon, then the voting system should prefer Daniel Webster.

Each of these conditions is of course a value judgement, but together they appeal to our intuition of what “fair and reasonable” means and seem like a sound set of requirements for a voting system. What Arrow proved is that satisfying all five of these conditions is impossible.

Arrow's Impossibility Theorem, Tao's Proof

We can define a voting system as a function which takes as input the voting preferences of each voter for a set of candidates, and returns as output the preference of society as a whole. Assume that voters are rational in the sense that each voter’s preference is a weak ordering of all the candidates. (To be mathematically precise, a voter’s preference is reflexive, complete, and transitive among the set of candidates.)

Let a quorum be a subset of voters such that, if everyone in the quorum votes for \(a>b\), and everyone outside of the quorum votes \(b>a\), then the social preference determined by the voting system will be \(a>b\). E.g., in a simple majority vote of 100 voters, a quorum would be a group of 51. So would a group of 76 or 99, but a group of 49 would not. Any quorum for a pair of candidates is decisive, and will force the social preference between those candidates.

Suppose our voting system satisfies all five of Arrow’s conditions, and that we have three candidates \(a,b,c\). Some observations:

• The set of all voters in society, which we can call \(V\), is always a quorum for every pair of candidates, by the Unanimity condition.
• A quorum forcing an outcome of \(a>b\), depends only on the relative rankings of \(a\) and \(b\), by the Independence of Irrelevant Alternatives condition.
• Different pairs of candidates may have different quorums. E.g., a quorum forcing \(a>b\) might not be identical to a quorum forcing \(b>c\).

Now suppose we have two quorums, a quorum \(S\) in which all members vote \(a>b\), and a quorum \(T\) in which all members vote \(b>c\). Suppose also that the voters who don’t belong to both quorums vote \(c>a\).

Because \(S\) and \(T\) are quorums, the social preference determined by our voting system will rank \(a>b\) and \(b>c\). By the Rationality condition, the social preference will also rank \(a>c\).

Note that the voters who belong to both quorums—the intersection of \(S\) and \(T\), \(S \cap T\)—vote \(a>c\). Because all the voters outside of \(S \cap T\) vote \(c>a\), and the voting system nonetheless results in \(a>c\), we have proved that \(S \cap T\)  in this scenario is a quorum for \(a\) and \(c\). This will be important shortly.

By the Non-Dictatorship condition, no single voter \(v\) can overrule everyone else’s preferences. Therefore, the set of all voters other than \(v\), \(V - \{v\}\), must be a quorum for any pair of candidates.

But there’s a problem here. If I have two of these subsets each excluding a different would-be dictator, \(V - \{v_1\}\) and \(V - \{v_2\}\), then I know that their intersection is a quorum from the earlier proof. This is true for any combination of candidate pairs.

And I can apply that intersection to another subset, \(V - \{v_3\}\), and then another, \(V - \{v_4\}\), and so on, until I’ve found the intersection of every would-be-dictator-excluding group. This final intersection is the empty set, \(\emptyset\), and contains no voters at all. By the earlier proof, the empty set must be a quorum, a bizarre and contradictory result: if the empty set is a quorum, then the set of all voters \(V\) is not, violating the Unanimity condition!

What we’ve shown is that Arrow’s five conditions for a fair and reasonable voting system cannot all be satisfied—no matter how we design our decision rule, situations can arise in which we must violate at least one of those conditions.

There are several ways to prove Arrow’s theorem; what I've presented above is a version of a proof by Terence Tao. I've actually glossed over a few details, so it doesn’t quite rise to the level of a formal proof, but my hope is that sacrificing a little rigor brings greater clarity, especially for those less familiar with formal logic.

Arrow's Impossibility Theorem, Geanakoplos's Proof

Let’s prove the theorem another way. It can be tough to grok a general result like Arrow’s theorem, and seeing the problem from multiple angles can help. Below is a version of a proof by John Geanakoplos.The idea of pairing these two proofs together came from a paper by Ashvin Swaminathan.

It’s easy to think of scenarios where a single voter is pivotal. Maybe your school board is divided four against four, and it’s up to you to cast the deciding vote. Similarly, we can have an extremely pivotal voter, able to vault a candidate from the bottom of the social ordering all the way to the top (or vice versa).

Note here that if all voters only rank a candidate \(b\) at the very top or bottom of their individual rankings, then the social preference must also rank \(b\) at the very top or bottom. Geanakoplos calls this the Extremal Lemma. We can prove this by assuming that the contrary is true (i.e., that the social decision could place \(b\) somewhere in the middle). Suppose that the social preference ranks \(a>b\) and \(b>c\). By the Independence of Irrelevant Alternatives condition, this will still hold even if every voter moves \(c\) above \(a\), because \(b\) occupies the top or bottom of every individual’s ranking and therefore the position of \(b\) in the social ranking won’t change. But now we have a sitution in which, by the Rationality condition,  \(a>c\), and yet, by the Unanimity condition, because every voter has moved \(c\) above \(a\), \(c>a.\) This is a contradiction, so our assumption must be false and therefore the Extremal Lemma must be true. Already this is disconcerting: the Extremal Lemma implies that the most polarizing candidates will always finish at the top or bottom, and never in between.

Let’s return to the idea of the extremely pivotal voter. Suppose we have three candidates \(a,b,c,\) and a voter \(v\) who is extremely pivotal for candidate \(b\). Let all voters rank \(b\) at the very bottom of their individual preferences. (The other rankings are arbitrary.) By the Unanimity condition, the social preference will rank \(b\) at the bottom. Now let the voters, one by one, move \(b\) from the bottom to the top of their respective rankings, leaving their other relative preferences unchanged. The extremely pivotal voter \(v\) is the first voter whose change will cause the social preference to change.

Let’s call the voter profile—the whole collection of individual preferences—just before \(v\) moves \(b\) to the top profile I. Similarly, denote by profile II the collection of all individual preferences just after \(v\) moves \(b\) to the top. Suppose then that voter \(v\) moves \(a\) above \(b\), so now \(a\) occupies the top individual preference for \(v\). Denote this last profile as profile III.

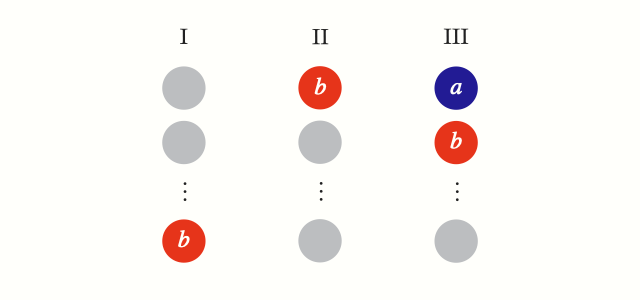
Observe that profiles I and III are identical with respect to \(a\) and \(b\): by the Independence of Irrelevant Alternatives condition, and because \(b\) sits at the very bottom in profile I, the collective decision for both profiles will rank \(a>b\). Similarly, profiles II and III are identical with respect to \(b\) and \(c\), resulting in \(b>c\). Because the collective decision for profile III ranks \(a>b\) and \(b>c\), then by the Rationality condition \(a>c\).

But something's wrong here. In profile III, voter \(v\) is in a position to dictate the social preference between \(a\) and \(c\), regardless of how anyone else has ranked those two candidates. Whereas \(v\) being extremely pivotal for \(b\) depends on how all other voters rank \(b\),  deciding the social preference between \(a\) and \(c\) is completely independent of how other voters rank those two candidates. Because the same arguments as above can be applied to any pair of candidates, we must conclude that \(v\) is a dictator, violating the Non-Dictatorship condition!

Measuring the General Will

Any voting system must sometimes violate at least one of Arrow’s conditions. For example, the plurality voting system that most of us are used to—sometimes called first-past-the-post—violates the Independence of Irrelevant Alternatives (which is why third parties in plurality voting systems can be spoilers).

It’s worth pausing for a bit of housekeeping. You may have noticed that I only proved Arrow’s theorem for three or more candidates. You can actually satisfy all five conditions with only two candidates, but in a way this avoids the hard problem of measuring the Will of the People: if we permit only two candidates on a ballot to avoid the contradictions of Arrow’s theorem, we still need a mechanism for deciding which two candidates should be allowed, and we’re right back to the original problem.

Arrow’s theorem also only applies to ordinal voting systems, which rank candidates, and not cardinal voting systems, which assign candidates a numerical score. But cardinal voting has similar impossible-to-satisfy conditions.

Perhaps the most common objection to Arrow’s result is that it’s a kind of technicality: yes we can’t always satisfy all five of Arrow’s conditions, but how often do these pathological voting scenarios really occur in practice? Unfortunately they occur far too often to dismiss. (See, e.g., the work of Gil Kalai.)

Our failure to measure the Will of the People isn’t due to flawed tools—we can’t fix the problem with a better voting mechanism or better turnout or so on—it’s inherent to the very nature of collective decision-making. Arrow’s theorem and its like show us that the “Will of the People” can’t mean any one thing. To the extent that we make it the basis of liberal democracy we actually undermine liberal democracy. The “Will of the People” is a vague, contradictory idea, waiting to be abused by every swindler and demagogue who comes along. But there are important distinctions to be made between the Will of the People and the Enlightenment ideal of self-government, and we can, I think, abandon the former without giving up on the latter.